How computers generate words

One very simple way we could generate words could be by using bigrams. We analyze pairs of consecutive words in training text to learn statistical patterns. For each word, the system calculates the probability of what should come next based on how often different pairs appeared together in the training data.

Let's say we have the following data:


the dog sat on the mat
the dog is on the floor
the dog is walking
the dog wants the bone
the dog wants the toy
the dog wants food

We can count how often a word appears after another:

First Word	Following Word	Count
the	dog	6
	mat	1
	floor	1
	bone	1
	toy	1
dog	wants	3
	is	2
	sat	1
sat	on	1
on	the	2
is	on	1
is	walking	1
wants	the	2
wants	food	1

Now, if we want to know which word is the most likely to come after dog we can look up the table and find the word wants.

To generate new text, the computer starts with an initial word, selects the next one based on the learned probabilities, then uses that new element to predict the following one, continuing this process to build complete words or sentences.

Modern LLMs use transformer architectures that can consider hundreds or thousands of words of context simultaneously. Instead of simple probability tables, LLMs use deep neural networks with billions of parameters that learn complex patterns and relationships across entire documents.

The core principle is similar though: predicting the next word based on statistical probabilities.

This is why LLMs need prompts like "You are a helpful assistant" to get started and longer, more detailed prompts typically produce better results. Each additional detail helps narrow down the vast space of possible responses to something more aligned with what you actually want.

Temperature

Temperature lets you control whether the AI plays it safe with common patterns or takes "creative" risks with less likely options.

Imagine we want to predict what comes after "the dog" based on these sentences. Looking at the data, after "the dog" we see:

"wants" - appears 3 times
"is" - appears 2 times
"sat" - appears 1 time

We need to convert these counts into probabilities.

The simple way would be dividing by the total (6), giving us: sat=17%, is=33%, wants=50%.

Instead, we will use a more sophisticated mathematical function called softmax.

Without getting into the math, softmax might turn our counts into something like: sat=5%, is=20%, wants=75%.

It amplifies the differences between common and rare words, making the most frequent patterns stand out more clearly. Temperature is a parameter that controls how much softmax amplifies these differences.

When you reduce the temperature, it makes "wants" even MORE likely to be picked while increasing the temperature flattens things out, making more likely to pick "sat".

Embeddings

Computers can only process numbers, not words. So how do we help them understand that "king" is related to "queen" but not to "banana"? This is where embeddings come in.

We could try assigning each word a single number:

word_ids = { 'king': 1, 'queen': 2, 'man': 3, 'woman': 4, 'banana': 5 }

But this fails because the numbers don't capture meaning. Is word #1 (king) more similar to word #2 (queen) or word #5 (banana)? The computer has no way to know.

Instead of one number, we give each word multiple numbers: a vector. Each number represents a different aspect of meaning. Imagine we measure three qualities:

[royalty, gender, fruitiness]

Now we can represent words as:

        
king   = [0.8, 0.9, 0.1]
queen  = [0.8, 0.1, 0.1]
man    = [0.1, 0.9, 0.1]
banana = [0.0, 0.0, 0.9]
apple  = [0.0, 0.0, 0.8]

In practice, we don't manually decide these numbers. Instead, we use machine learning to automatically discover dimensions that capture meaning by analyzing how words are used in millions of sentences. The resulting embeddings enable computers to understand word relationships well enough to power modern AI applications.

Now computers can calculate which words are similar by measuring distances between vectors:

Distance(king, queen) = small → related
Distance(king, banana) = large → unrelated
Distance(banana, apple) = tiny → very related

Let's have a look at this:

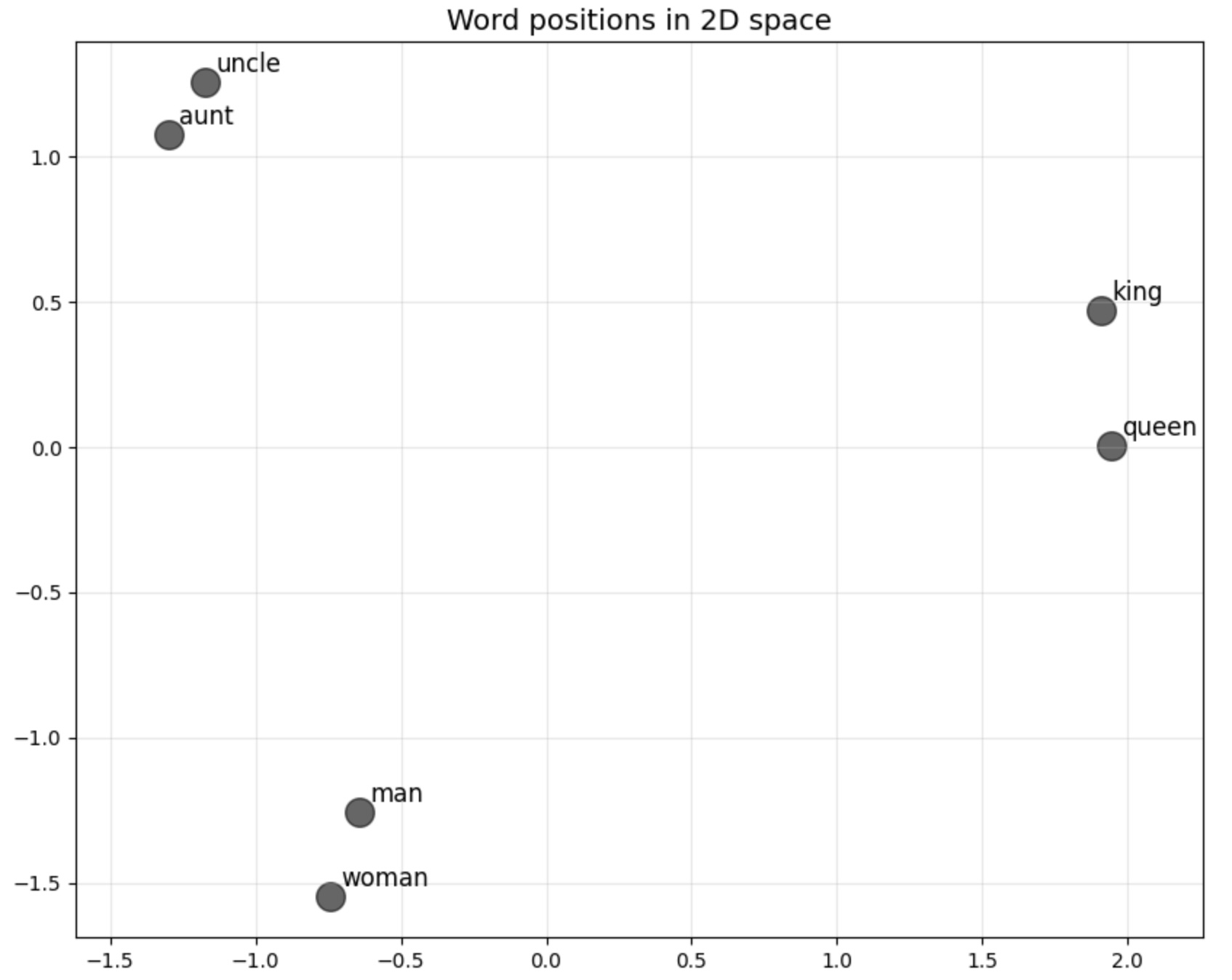
Look at the distance and direction between "man/king" and "woman/queen".

Imagine you don't know the word "aunt" and you're trying to find it. You know that an uncle is a man who is your parent's sibling.

Using vector arithmetic, you can calculate: woman + (uncle - man) = aunt
This works because (uncle - man) captures the "parent's sibling" relationship, and adding it to "woman" gives you the female version.

We can use this for many things such as:

England + (Paris - France) = London

However, this doesn't always work:

Canada + (Paris - France) = Toronto

Why does this happen? Word embeddings learn from how often words appear together in text. Toronto appears with "Canada" far more often than Ottawa does, so the model associates Toronto more strongly with Canada. The embeddings capture statistical patterns, not factual truths.

This is exactly how modern AI systems can "hallucinate". They find the most statistically likely answer based on patterns in their training data, which isn't always the factually correct answer.

Tokens

If LLMs used words, the model would need a vocabulary of millions of entries to cover all possible words in all languages. Instead, they break text into common chunks that can be recombined.

This approach also handles variations elegantly. Rather than storing "run," "runs," "running," "runner," and "runnable" as completely separate tokens, the model can learn the root "run" and the patterns of "-s," "-ning," "-ner," and "-able".

Now you can understand why LLMs are having a hard time counting the letter "r" in strawberry. They never actually see the word, only pre-chunked tokens like "straw" and "berry".

To the model, "straw" is just an indivisible unit not a sequence of letters s-t-r-a-w. Then it learned that the token "berry" appears in contexts about fruits, follows certain patterns and combines with other tokens in meaningful ways. But it never learned that "berry" contains b-e-r-r-y.

Because tokens are just chunks of information converted into numbers that the model can process, images can be divided into small patches and audio into tiny time slices or notes. Each piece becomes a token. The same mechanism that predicts the next word can now predict the next image patch or musical note.

Attention

Attention is the secret sauce behind modern language models. At a high level, it lets the model decide which tokens to "focus".

For example, choose the next word between supermarket and mechanic:

Yesterday, I drove my broken car to the {?}"

You subconsciously assign more importance to the words broken car than yesterday.

Older models struggled with long sentences. The meaning of early words would fade by the time the model reached the end. Attention solves this by creating a direct shortcut to every word in the context.

It does this by creating three special vectors for each word:

Query: This is like a question the current word asks. For our {?} token, the query is essentially, "Given the context, what kind of place am I?"
Key: This is like a label or a "keyword" for each word in the sentence. The word "car" would have a key that says, "I am a vehicle," and "broken" would have a key that says, "I describe a state of disrepair."
Value: This contains the actual meaning or substance of a word. It's the information that gets passed on if a word is deemed important.

The model takes the Query vector for {?} and compares it with the Key vector of every other word in the sentence. This comparison is usually done using a dot product:

Q_{?} ⋅ K_{car} will produce a high score because the question "what kind of place am I?" is highly related to the keyword "I am a vehicle."
Q_{?} ⋅ K_{broken} will also produce a high score because the context of "broken" is critical.
Q_{?} ⋅ K_{yesterday} will produce a low score because the time aspect isn't as relevant to the type of place.

After softmax, the words "broken" and "car" will have high attention weights (e.g., 0.5 and 0.4), while words like "I" and "yesterday" will have very low weights (e.g., 0.01).

At the end, the model multiplies the attention weights for each word by that word's Value vector. Because "broken" and "car" have high weights, their Value vectors will dominate this context vector.

Remember about the embeddings earlier? The vectors for mechanic, garage, and repair will be clustered together. The vectors for supermarket, store and groceries will be in another cluster, far away from the first one.

When the attention mechanism creates a context vector for our sentence, that vector points to a specific spot in this semantic space. Then the model picks the most probable word from that region.

Fine-tuning and LoRa

Imagine a neural network as a massive machine filled with adjustable knobs. Each knob controls how information flows through the system.

Input         Hidden Layers           Output
─────         ─────────────           ──────

[●]           [●]   [●]   [●]         [●]
 ├─────────────┼─────┼─────┼───────────┤
[●]           [●]   [●]   [●]         [●]
 ├─────────────┼─────┼─────┼───────────┤
[●]           [●]   [●]   [●]         [●]
 └─────────────┴─────┴─────┴───────────┘

You move the input knobs on the left and the output on the right changes based on their positions. During training, we figure out exactly how to set all the knobs in the middle (hidden layers) so that any input knob configuration produces the correct output.

You want to change the output but you don't want to touch the knobs in the middle because it would be very time consuming to figure out what works and you might break something.

Instead, You take the generated output of the big model and change it to your liking. To figure this out, you train your own small machine. You take the input, run it through the big machine, and then run it through your smaller machine to figure out what adjustments to make to get the desired output.

Your small machine learns: "When the big model says X, I need to nudge it toward Y instead".

Input    Hidden Layers  Output  Adapter   Final Output
─────    ─────────────  ──────  ───────   ────────────

[●]───┬──[●]─┬─[●]─┬──────[●]───┬─[●]───┬──►[●]
      │      │     │            │       │
[●]───┼──[●]─┼─[●]─┼──────[●]───┼─[●]───┼──►[●]
      │      │     │            │       │
[●]───┴──[●]─┴─[●]─┴──────[●]───┴─[●]───┴──►[●]
          ↑     ↑                  ↑
          │     │                  │
        Don't touch           Train these

Now, this helps visually represent what is happening but what LoRA actually does is adding small trainable modules inside the big model at many layers, not just at the end.

Input    Hidden Layers (with LoRA)    Output
─────    ─────────────────────────    ──────

[●]───┬──[●+△]─┬─[●+△]─┬─[●+△]───┬──►[●]
      │        │       │         │
[●]───┼──[●+△]─┼─[●+△]─┼─[●+△]───┼──►[●]
      │        │       │         │
[●]───┴──[●+△]─┴─[●+△]─┴─[●+△]───┴──►[●]
          ↑         ↑       ↑
          │         │       │
      Original + Small LoRA adapters
      weights    at each layer

LoRA's distributed approach is more powerful because it can influence processing at each stage of the network, not just post-process the final result.

This is how we can take a massive trained model and teach it new things without starting from scratch. For example, the big model already knows language or how to draw and LoRA nudges it toward a specific style (e.g Gordon Ramsay or Studio Ghibli).

You can mix and match them and adjust their strengths by turning the their input knobs (50% anime style, 30% cyberpunk, 20% vintage).

They're incredibly small (only needs a few million parameters) and cheap (~$10 - $100) compared to the base models they modify. You can literally train one on your gaming computer at home.